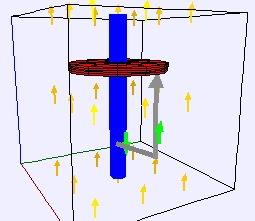
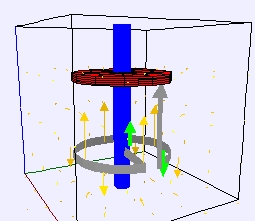
Faraday Disk Dynamo Model

The EJS Faraday Disk Dynamo shows a conducting disk that rotates in a magnetic field. This produces a current (homopolar generator) and for certain configurations, it is a self-exciting dynamo. A self-exciting dynamo is the mechanical analog of a proposed mechanism to produce the earth and sun's magnetic fields. Ejs must be installed to explore and change the model.

Exercises:

1. "Ext B" and "Constant ω": Run the simulation first with a uniform external magnetic field (yellow-orange field vectors) "Ext B" and constant angular velocity "constant ω". The green arrows show the direction of the current as the disk rotates and the plot shows the current (green) and angular velocity (red) as a function of time. Explain the reason for the current flow (and the associated direction).
2. Optional calculation: This is a clearly a way to generate electricity, but it can require a fairly large dynamo.  Input different values for the constant angular velocity, ω. Notice the associated values of the current produced.  Show that the induced emf on a rotating disk in a uniform field is Br²ω/2 where B is the external magnetic field, r the radius of the disk and ω, the angular velocity. If the magnetic field is 1 T (fairly large), the resistance of the circuit carrying the current is 1 Ω and the plot shows the current in units of Amps and angular velocity in units of radians per second, what is the radius of the dynamo disk?
3. "Ext B" and "Constant torque": This time, instead of a constant angular velocity, assume a constant applied torque, τ (start with τ=1). Without an external magnetic field (and generated current), you would expect the angular velocity to increase (or decrease) steadily. Why? In this case, however, since the system settles down to a constant angular velocity, there must be another torque acting on the system. Show that the additional torque is due to the force (F = iLxB) due to a current flowing in a magnetic field and is equal to i ∫ B r dr where r is measured radially on the disk.
4. "Coil" and "Constant ω": Neither of the previous situations are self-exciting dynamos. In a self-exciting dynamo, the current produced induces a magnetic force which changes causing a changing current thereby setting up a feedback loop that keeps the current going without an external magnetic field (once there is an initial non-zero current/magnetic field). Choose "Coil" and "constant ω" to see the geometry of a system that has the potential to be a self-exciting dynamo. Try values of ω greater than 1 and less than 1.  For values greater than 1, it seems like this might be a way to generate lots of current with no work.  What is the catch? (Hint: Look at the value of the torque and consider what is necessary to keep ω constant at larger and larger currents.)
5. "Coil" and "Constant torque": Try some different values of the initial ω when there is a constant external torque. When τ = 1, can you find initial values of ω where the disk changes its direction of rotation and the magnetic field swaps direction? This is a requirement for a model of the magnetic field of the earth or sun (since the magnetic field has changed over time). Repeat for another value of the torque.
6. "Capacitor" and "Constant torque": By adding in a capacitor (and the additional non-linear differential equation), the system can become chaotic. The plot now also shows the charge as a function of time (in blue). Try an initial value of  τ=1 and ω= 3.0 and observe the phase space plot (plot of current, charge and angular velocity)-- this is similar to the Lorenz attractor. What hallmarks of a chaotic system does this system exhibit?
   

• Hecht, Physics: Calculus, 2nd edition, Brooks Cole, Chapter 20 (2000).
• Sir Edward Bullard, "The stability of a homopolar dynamo," Mathematical Proceedings of the Cambridge Philosophical Society, 51 (1955) 744-760.
• Raymond Hide, Anne C. Skeldon and David J. Acheson, "A study of two novel self-exciting single-disk homopolar dynamos: Theory" Proceedings fo the Royal Society A, 452 (1996) 1369-1395.
• Irene Moroz, "The Hide, Skeldon, Acheson dynamo revisited," Proceedings of the Royal Society A, 463 (2007) 113-130. 

Credits:

The Faraday Disk Dynamo Model and Exercises were created by Anne J Cox using the Easy Java Simulations (EJS) authoring and modeling tool. 

You can examine and modify a compiled EJS model if you run the program by double clicking on the model's jar file.  Right-click within the running program and select "Open EJS Model" from the pop-up menu to copy the model's XML description into EJS.  You must, of course, have EJS installed on your computer.

Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.