Rail Gun Model

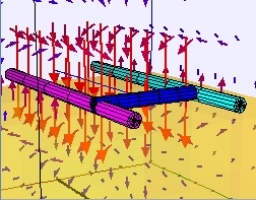
The EJS Rail Gun Model shows a rail gun created by running current through long rods with a cross-rod accelerated due to the external field from the current in the rails. It also shows the magnetic field that the cross-rod experiences. Students can adjust the current in the rails and rod as well as the spacing between the rails. 

Exercises:

1. Run the simulation. The cross-rod, resting on frictionless rails, initially begins at rest and is accelerated due to the magnetic field.  You can zoom in (Shift-Click-Drag), rotate (Click-Drag) or pan (Ctrl-Click-Drag) the 3D views. Pause the simulation before the cross-rod drops leaves the rails. What is the direction of the magnetic field due to the current in the (the magnetic field outside each rail is approximated as the field from the end of a very long wire: B = μ₀I/4πR)? Looking at the magnetic field, what direction is the current flowing through the blue cross-rod (from the pink rail to the cyan rail or vice versa)?
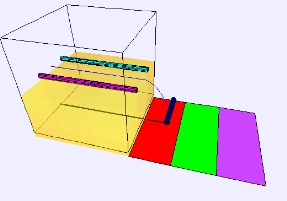
2. When the cross-rod lands, it has fallen 5 cm down from the yellow box to the carpet. The simulation reports the distance it travels from the edge. How does this distance depend on current (in amps) and distance between the rods (in cm)?
3. To calculate the external field of the cross-rod, the simulation uses the value of the magnetic field due to the two rails in the middle.  Treating each rail as a long wire gives a field at the end of each rail of B = μ₀I/4πR (where R is the distance from the rail). Show that B = (μ₀ I/4π)(4/L) is the field in the mid-point (a distance L/2 from each rail) between the two rails (that would be experienced by the center of the rod). Assuming this constant magnetic field, what is the value of the force on the rod? If the rails are 10 cm long and each of the landing mats is 4 cm wide and the mass of the rod is 1-g (independent of its length), what current is required for the rod to land where the red and green mats meet (after falling a distance of 5 cm down)? the green and purple meet? the edge of the purple? Show your work and verify your answers using the simulation.
4. Click on the Show B(x) check-box. This shows the magnetic field as a funciton of position between the rails. Given that the simulation uses the value of the magnetic field in the middle of the rails, how would you expect the simulation to change if the variation in the magnetic field were taken into account? Specifically, what would happen to the trajectory of the cross-rod?
5. Show that the equation of the field as a function of position between the rails is given by B(x)= (μ₀I/2π)(L/(L²-x²)) where x = 0 is in the center between the rails.

• Giancoli, Physics for Scientists and Engineers, 4th edition, Chapter 28 (2008).

Credits:

The Rail Gun Model and Exercises were created by Anne J Cox using the Easy Java Simulations (EJS) authoring and modeling tool. 

You can examine and modify a compiled EJS model if you run the program by double clicking on the model's jar file.  Right-click within the running program and select "Open EJS Model" from the pop-up menu to copy the model's XML description into EJS.  You must, of course, have EJS installed on your computer.

Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.