Helmholtz Coils

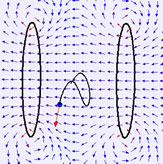
The EJS Helmholtz Coils Model shows a the magnetic field between two circular coils of wire.  The default configuration, known as a Helmholtz coil, sets the separation distance D equal to the coil radius R.  These values produce a nearly uniform magnetic field B between the coils

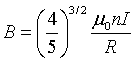
where I is the current, n is the number of loops in each coil, and μ_o is the magnetic permeability.  The model includes the simulation of a charged particle trajectory in the vicinity of the coils.

Exercises:

1. In what direction is the current flowing in each loop? (Draw a sketch of the current.)
2. For a uniform field near the center, set D = R. Compare the motion of a charged particle when R = D and when R<<D. Explain the differences (look at the vector fields).
3. For R = D, if you start with vy = 0, can you get almost circular motion? Why?
4. The set-up for a standard e/m experiment uses Helmholtz coils (with R=D to create a nearly uniform magnetic field) to move the electrons in a circular path after they are accelerated to a known velocity by an electric field. For this simulation, the particle is a positively charged particle (how can you tell?). Set vx=vy=0 and pick an initial value for vz (in cm/microseconds) and measure the radius (in centimeters) by noting that the sliders change their value to indicate the location of the charged particle. If the charged particle is an alpha particle (charge = 2e, mass=4u), what is the value of the current in each coil if each coil has 200 loops? If the particle had a larger charge to mass ratio, would the current need be larger or smaller for the same size circular path? Explain.
5. Show that the first and second derivative of the magnetic field on-axis at the center is equal to zero if D = R. Why does this produce a nearly uniform field near the center?

References:

Because Helmholtz coils are often used in experiments to produce nearly uniform magnetic fields, their use is discussed in many experimental physics laboratory manuals.

• Adrian C. Melissinos and Jim Napolitano, Experiments in Modern Physics, Second Edition, p275 and p286.

The analytic expression for the on-axis magnetic field is straightforward to derive and this derivation is often assigned for homework in physics textbooks.

• Ray Serway and John Jewett, Physics for Scientists and Engineers sixth edition, pages p963.
• David Griffiths, Introduction to Electrodynamics, third edition, p249.

A challenging theory problem is the derivation of the off-axis magnetic field in terms of elliptic integrals.  This computer model computes the magnetic field using the Biot-Savart law and performing a numerical integration around each coil.

Credits:

The Helmholtz Coils Model was created by Fu-Kwun Hwang at National Taiwan Normal University using the Easy Java Simulations (EJS) modeling tool. It was adapted to EJS version 4.1 by Robert Mohr and Wolfgang Christian at Davidson College. You can examine and modify a compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open Ejs Model" from the pop-up menu.  You must, of course, have EJS installed on your computer.

Information about Ejs is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.